Hello NathanE
Here is an approach for the speed of the air that “hits” the pilot of the Portable Flyer at hovering.
Quote from
NASA “Propeller Thrust” at
https://www.grc.nasa.gov/WWW/K-12/airplane/propth.html :
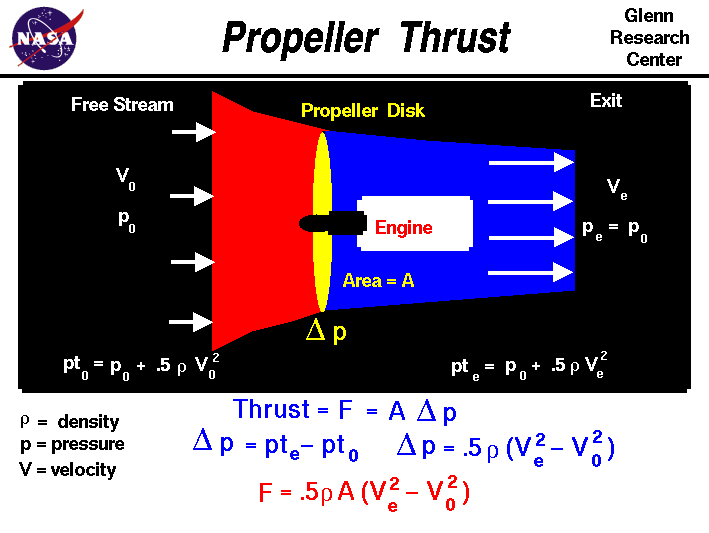
Simple Momentum Theory
Turning to the math, the thrust F generated by the propeller disk is equal to the pressure jump delta p times the propeller disk area A:
F = delta p * A
Etc, etc . . . (the link has the complete analysis)
Substituting the values given by Bernoulli's equation into the thrust equation, we obtain
F = .5 * r * A * [Ve ^2 - V0 ^2]
End of quote.
At hovering V0=0 (zero vehicle velocity), so the above formula becomes:
F = .5 * r * A * Ve ^2,
i.e. Ve=(2*F/ (r*A))^(1/2)
With your F=1,500Nt, r=1.225Kg/m3 and A=1.2m2,
the Ve (i.e. the speed of the air that "hits" the pilot of the Portable Flyer) is calculated at
45m/sec (100mph, 160Km/h).
Hello Tommy Cookers
NASA at
https://www.pattakon.com/Fly_files/NASA ... Thrust.pdf gives a "formula" / relation for the Static Thrust of airplane propellers.
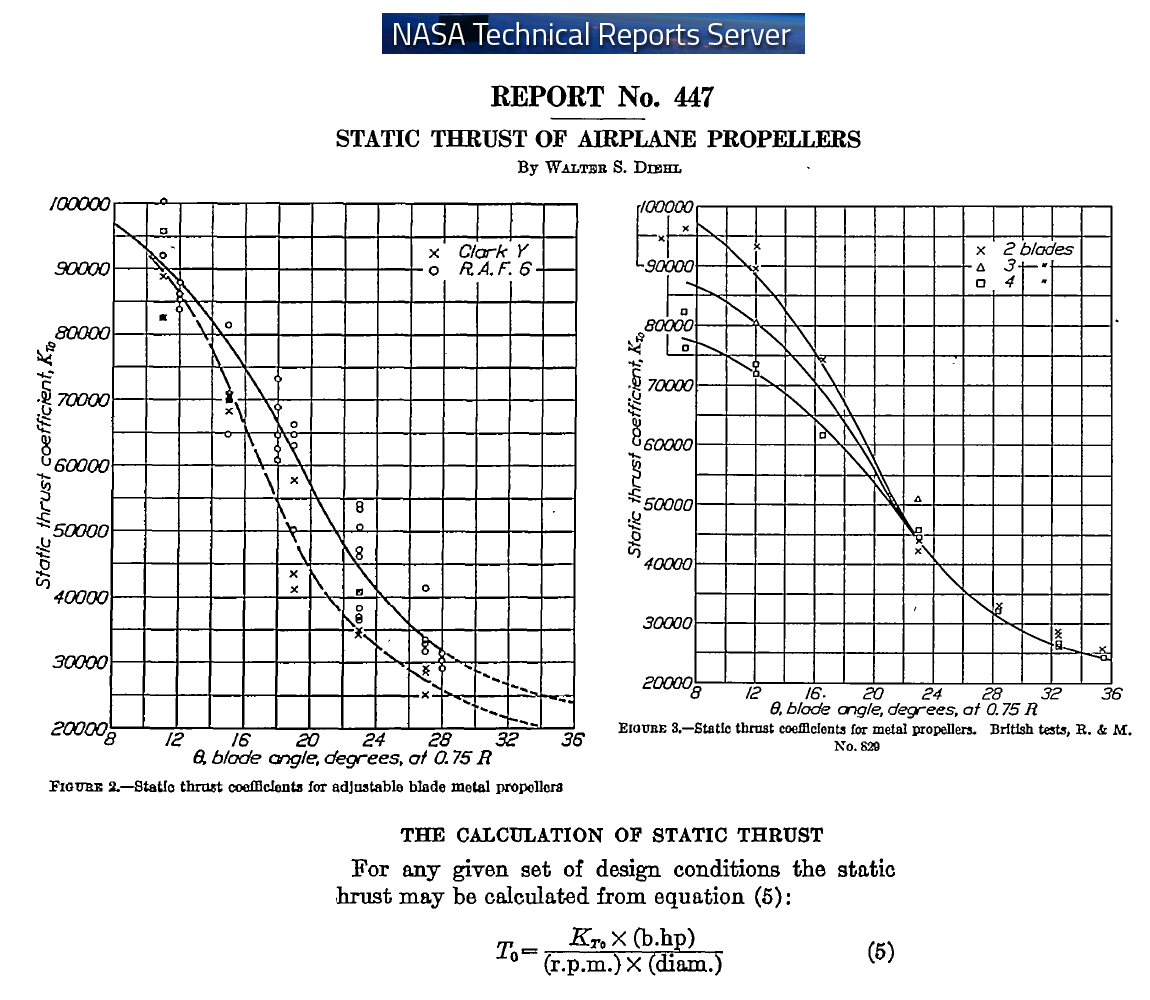
For instance, a propeller having 42” (3.5ft) diameter, 30” pitch (the θ about 17 degrees at 0.75R, giving a K coefficient around 60,000), revving at 3,000rpm absorbing 30 bhp, gives a static thrust of:
T = 60,000 * 30 (bhp) / (3,000 (rpm) *3.5 (ft))=170lb = 780Nt (=78Kgf).
With smaller (into some limits) pitch, the power absorbed (same rpm of the propeller) decreases, but the coefficient K increases, giving, say, a similar Static Thrust.
Another reading of the above is: Keeping the propeller rpm constant, by varying the pitch what you can do is to reduce or to increase the power required for the "same" Static Thrust, but the change of the Static Thrust due to the variation of the pitch is small.
This is the reasoning behind the PatPitch:
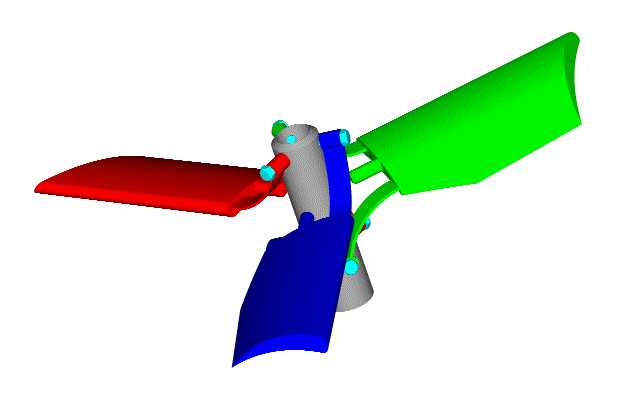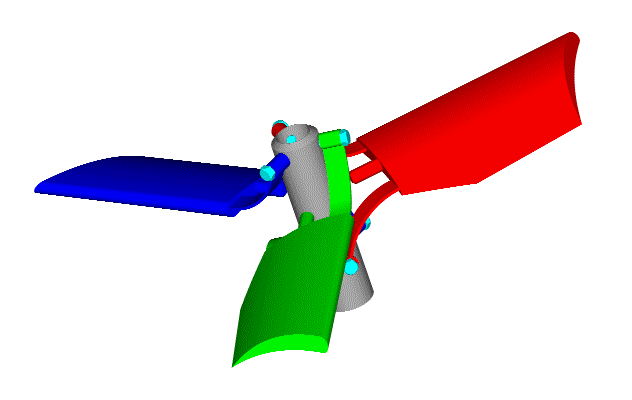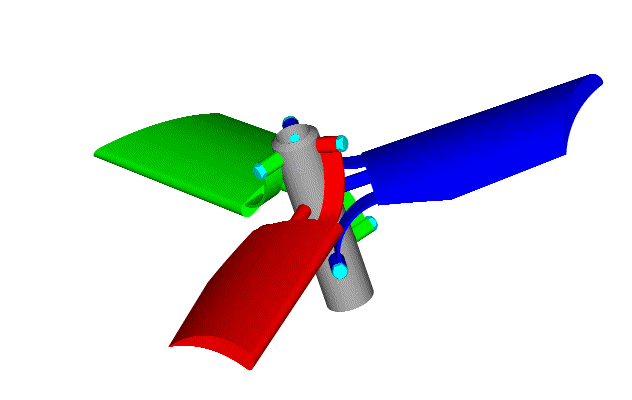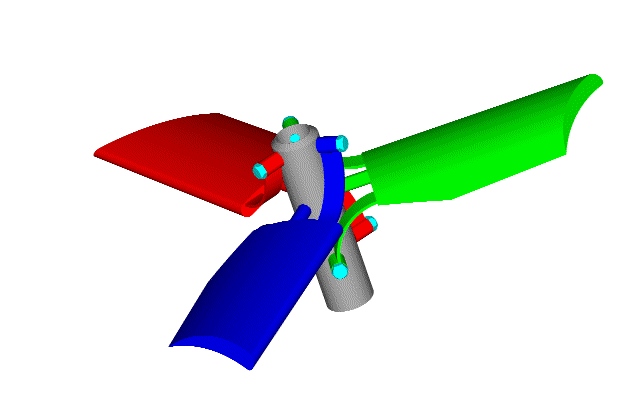
At hovering ("medium" engine (and propeller) revs), the PatPitch keeps the propellers at a lower pitch; at high cruise speeds ("high" engine (and propeller) revs), the PatPitch keeps (with the heavier centrifugal forces acting on the blades) the propellers at a larger pitch, allowing substantially higher top speed.
Hello J.A.W.
I can't get what you mean by "Manolis can draw the flak, as you fly under the radar, surely?"
Thanks
Manolis Pattakos






