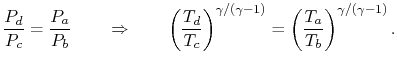xpensive wrote:A turbo indeed takes power from the xhaust to power the compressor, but actually not that much;
Power is flow times pressure; P(W) = Q(m^3/sec) * p(Pa)
Let's say that our 1.5 turbo-engine is revving at 12k at an absolute pressure of 2.5 Bar, that means that it's fed with 150 dm^3 per second at a boost of 0.15 MPa, if we simplify things with a 100% filling rate.
P = 0.15 * 0.15*10^6 = 22.5 kW
Guessing an efficiency of both turbine and compressor of 0.95 brings the total loss to 25 kW.
With a mechanical output of 590 kW (800 Hp), 25 kW is about 4%, what impact will that have on the sound?
A turbo power calculation is slightly different.
It's based on pressure ratio between inlet and exhaust and the inlet temperature.
Turbine work is more like this: efficiency * Cp air * delta T , this is from the brayton cycle.
delta T is between inlet and outlet. Turbine efficiency is given by the manufacturer. This is the simple equation but is accurate enough.
This equation is not enough, you need this relation:
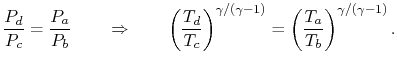
it can spin around to this : T2/T1 = (P2/P1)^ ((k-1)/k) (2)
in this case, T2 is air temperature after compression, T1 is inlet temp.
usually you know the pressure ratio (p2/p1), atmosphere is 1 bar, and compressing to 2.5bar. ratio is 2.5.
Lets say air temp is 30 degrees C, 303 Kelvin. Turbine inlet is 1000 C, 1273 K.
Our compressor efficeicy is say 80% and so is the turbine.
compressor Eff = 0.80 = ideal compressor work/ actual work
0.8 = Cp(T2ideal-T1)/ Cp (T2actual - T1) ;
we know T1 but will need to find what the temp is after compression in turbo air side.
we rearrange eq2 T2 = T1 (P2/P1)^ ((1.4 -1)/1.4) = 303*[2.5^(0.4/1.4)]
= 394K , 121 degrees C.
but becuase it is not ideal we use efficiency equation,
0.8 = Cp(T2ideal-T1)/ Cp (T2actual - T1)
0.8 = (394 - 303)/ (T2- 303) , T2 = 416.75K = 143.75 C
doing the exact same equations for the turbine (pressure ratio is now ,1 bar/ 2.5 so it's 0.4 since the turbine is dropping pressure not building it, ideal turbine exhaust temp T4 works out to: 980K or 706 C.
from efficiency equation: T4 is actually 1038.6 K or 765.6 C
we have the temperatures now we can find the work.
Turbine work = Cp*(1000-765.6) Cp for air is 1.04,
= 243.7 KJ/kg.
if you multiply this by the mass flow you get the power the turbine takes.
using 0.45kg/s
243.7kJ/KgK * 0.45kg/s = 2437 kJ/s = 109.65 KW
Results could be completely different without taking into account temp, press, efficiency and specific heat.