Well, I adhere to Tim opinion: what you read is plainly wrong.
Summary: if the width is not important, why slicks? You could use rain tyres and get the same grip. So, get a grip... ha, ha.
Now, one of my legendary short posts. I disagree with Tim in one thing: it's not "horribly" non-linear, it's beautifully non-linear.
What's going to be horrible is this post, because of its length, but I honestly think that any aspiring racer in the XXI century should know this. In short, the best graph I could make of the data available to me is this one:

Why? Well, kep reading.
The weight of the car is not the only thing that limits the adherence, but the interlocking and sticking you get between tires and asphalt. If you could develop a perfect interlocking (think of a "funicular" with gears) you would, in theory, get infinite "friction factor". Same consideration applies if you could develop perfect "stickiness" between the asphalt and the tire. This is not as farfetched as you could think, there are new materials based on gecko's feet that help to develop this "microeffect" of fractal grip.
In the end, friend,
F1 and dragster tires "work" mainly by adhesion. Therefore, slicks.
I give some links again:
Why Tires Grip The Road: New Theory Reduces Testing
..dry-weather tires in Formula One racing ... exude resins and actually even out irregularities in the asphalt, thus considerably improving the area of contact... Racing tires are literally sucked dry.
As you can imagine, the wider the tyre, the largest the amount of fluid the tyre "sweats".
So, what you try to do with a racing tyre is to "fill" the spaces among the irregularities in asphalt.
There is a new theory, some years old by now, that has completely superseded Coulomb's. If you wish, read here.
Elastoplastic Contact between Randomly Rough Surfaces
As, in my experience, NOBODY follows links around here, there you have my explanation. I do not doubt many people will point out my errors... sigh.

Essentially, what Bo Persson (blessed be his soul!) proved is that if you see the asphalt as a fractal surface (remember fractals?) the area of contact between tyre and asphalt increases proportional to the force you put on the tyre. This image shows how small is the real contact area under regular loads:

There are several "modes" of developing friction, from an "interlocking" mode to a "sticky" mode. The interlocking works at macroscopic scales, the stickiness work at molecular scales.
This means that the tyre "grabs" the small rocks in the asphalt and also "sticks" to the smooth parts of the tarmac. In the following image, which I also repost, the "interlocking" occurs when you see the tyre at the 5 mm level (macrotexture) while the "stickiness" happens at the microtexture level.

Therefore, the references to the "physics of smooth bodies" don't apply: the smoother the surface, the more adhesion you can develop by chemical, electrostatic or even dispersive or diffusive mechanisms (and less macroscopical interlocking or "mechanical adhesion"), which are the five mechanisms developed to explain adhesion.
There is an optimal asphalt-and-rubber texture where the sum of the five modes of adhesion reach a maximum.
Finally, slip angle is what makes the tyre grip. An infinitely narrow tyre has no slip angle... This is the image from "The Racing and High-Performance Tire", that shows how slip angle works. For the non mathematically inclined, the idea is that a tyre works by twisting. So, a wider tyre has a more "gentle" twisting, so the erosion (wear) is smaller.
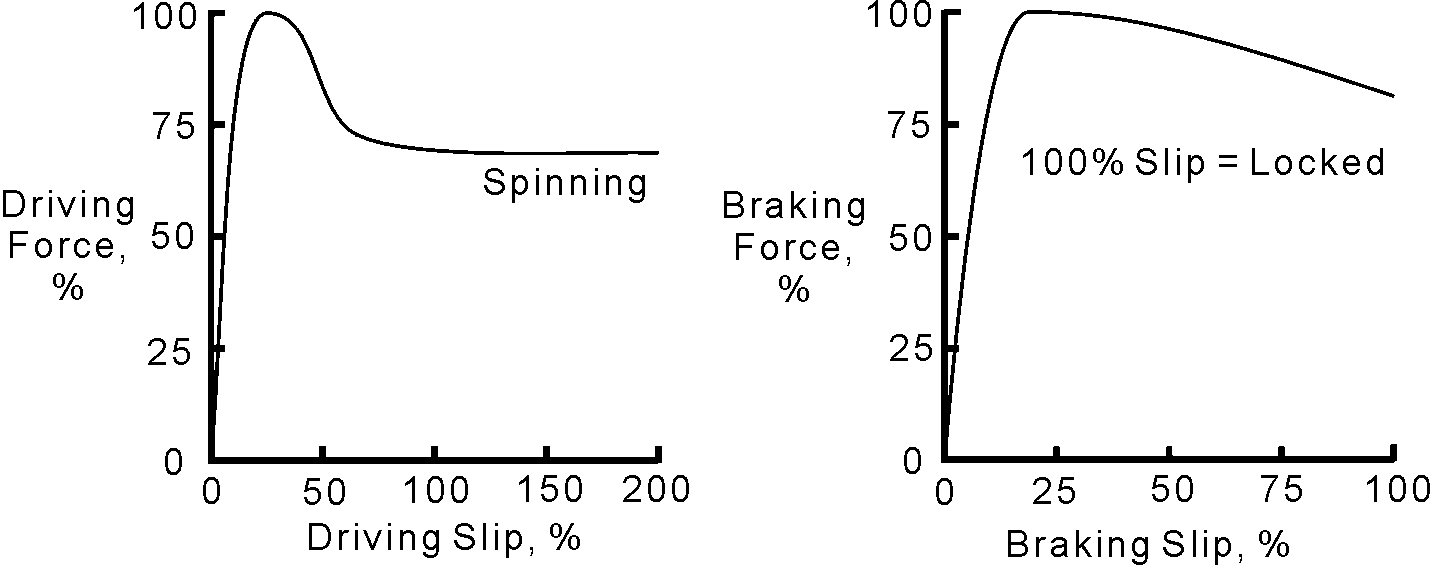
So, why are not infinitely wide tyres used in racing?
Well, the problem is aerodynamic, as you can imagine. So, the width of a tyre is a compromise between the aerodynamic drag you "pay" and the "stick" rewards you get from a wider tyre.
What are the rationals? Here you have a "small" history of tribology.
The first known theory of friction was written by Leonardo Da Vinci around 1450. He studied a lot of things about friction, including wear, bearing materials, plain bearings, lubrication systems, gears, screw-jacks, and rolling-element bearings. Almost two centuries before Amontons' Laws of Friction were introduced, he had discovered them.
Unfortunately his writings were lost and unread for two centuries. After Leonardo, the first guy (and almost the last...) to explain friction was Amonton, around 1650. He rediscovered Leonardo's principles of:
- friction proportional to weight and
- friction independent of the area of contact
Coulomb, around 1750, introduced the idea of:
- kinetic friction independent of speed of displacement
These three laws can be summarized in this graph, which, unfortunately is most of what the majority of people learn about friction:
Some engineering courses never go beyond this graph. Sad.

Then after another century, Reynolds (and a russian guy whose name I cannot remember) came up with an equation (unchanged since 1880 or so) of:
- friction in fluids proportional to sliding velocity and bulk viscosity and inversely proportional to thickness of film
A few years later Stribeck (not sure about the name) came up with the Stribeck curve that explains that when the film is very thin, Reynolds equation fails. He stated that:
- the area enlarges because the contact surface deforms elastically and the film, with a larger area, can support the weight.
Then, after 50 years (we're getting some speed here... ), Hardy, around 1920, came up with the idea of very thin films like this:
- asperities coming in contact, breaking and then reacting chemically with the lubricant, thus creating a tenacious layer of lubricant and small chips of material that supports the weight and prevents further wear (I swear I'm not making this up... ).
Hardy findings about films inspired some people to try to understand what happens in dry friction. Finally, a few years later, a guy named (I think) Bowden came up with the concept of friction by adhesion. Another guy called Desangulier in Coulomb's time had the same idea but nobody heard him because of Aumonton 2nd law (friction independent of area), so people devoted to purely geometric explanations (interlocking of asperities). Bowden discovered that Tim is right and:
- friction is created by adhesion of solids because of electric charges.
It might sound incredible, but asperities in solids deform above a critical shear strength, which depends on the adhesive forces of the two surfaces in contact. That adhesive force, the one that "crushes" the asperities, is created by electric charges.
Yes, I know, it sounds like science fiction, but I'm dead serious.
The relationship with the load is not lineal but is, as showed in the first graph of this "summary": 
F = L^2/3 (that is, friction is proportional to load elevated to two thirds)
The inconsistence with Aumonton's first law (friction proportional to load) is explained because the real contact area varies under load. Why nobody noticed in five centuries beats me.
Once electronic force microscopes were developed, around 1950, Bowden (and Desangulier) were vindicated, because measurements were precise enough to validate their theory. Thus, Tim is right.
That's most of what I know about friction. and you can stop reading now.
If someone is interested in visualize (that's what distinguishes engineers!) what's going on, please, come with me for a couple more paragraphs and imagine what happens if you become really tiny: your weight decreases as the cube of your height does (a person half as tall, half as wide and half as deep, weighs eight times less!), right? However, if you're half as tall, your surface is only one quarter of the original one. For example, let me tell the story about Gauss famous observation on the size of things.
Gauss teacher told the class (in primary school, according to legend) that the Universe could grow slowly to one million times its actual size and nobody would notice. Gauss answered that it was not true, because all the picture frames would fall from the walls. Their weight would increase to the cube, but the area of the strings holding the pictures would increase to the square and they would not be resistant enough to hold the pictures to the walls. Incidentally, that's why ants and spiders have such thin legs and elephants have sturdy ones, but I digress.
So, if you're a really small asperity, you have a very large surface compared with your weight. If your ten thousand times (2^13) smaller than a person (around 0.2 mm), your weight/surface relationship is 10.000 times larger (I think). Persons are taller than wider: this means that electric charges migrate to the pointy parts (by electromagnetic laws: that's why lightning rods are pointy). Like this:
Small clay particle with positive electric charges in the pointy parts

Thus, any point in a microscopic asperity of the tyre (charged positively) adheres to the sides of the microscopic asperities of the track (charged negatively). Its weight is ridiculously small compared with the surface, thus the electric forces are immense compared with gravitational forces at these scales.
Tyres adhere to asphalt by electricity. QED.
Finally, in the last ten years friction has been explained by quantum theory. In the improbable case that someone is interested in "The Master Equation" of friction, there you go:
http://www.sbfisica.org.br/bjp/files/v27_214.pdf
Friction Quantum Theory Master Equation. If someone can explain it in simple terms, be my guest!

As usual, sorry for going OOT and sorry for the length of the post.. perhaps someone will read al this voluntarily! On the other hand, my poor students have no choice.












