A complex sound can be broken down into a series of superposed sine waves. By shifting a time domain ‘real sound' into the frequency domain to show a spectrum, via the use of a Fourier Transform.
Real noise will have a host of orders, and random background masking noise. Some tones will stick out above this and be audible. For ease of analysis you can simplify this by picking out the most prominent tones, and modelling them as superposed sine waves to get an approximation of the sound we will hear.
The first part of the post is simply a proof that the method works, the second part contains a comparison of the V6 and V8.
Wolfram Alpha will be used to plot and create audio tones.
Worked Example:
Plot of a Complex Tone Consisting of a Fundamental Sine Wave + 3 Overtones
sin(t) – Fundamental
sine(2t) – 1st Overtone
etc.
http://www.wolframalpha.com/input/?i=pl ... 284t%29%29
Same Waveform With a Phase Change
The phase change chosen for this was 90degrees (or pi/2 radians).
sin(t+pi/2) - Fundamental
http://www.wolframalpha.com/input/?i=pl ... %2F2%29%29
Sum of the Two Complex Waveforms using Superposition
This plot shows both complex tones, superposed together.
http://www.wolframalpha.com/input/?i=pl ... %2F2%29%29
The second method, to show that you can break down the tones into fundamental sine waves and do the same operation.
Fundamental Sine tone + fundamental tone + pi/2 Phase.
Also note, that summing these two sine waves produces a sine wave of the same frequency but of a third phase.
http://www.wolframalpha.com/input/?i=pl ... %2F2%29%29
This sound would be exactly the same, as the ear itself cannot detect the phase of a single tone.
(For the moment, auditory phenomena such as beats, and auditory illusions is beyond the scope of this point)
Plot of the simple tones + their phases summed together using Superposition.
This plot shows the two phased sine waves summed together.
Sin(t)+sin(t+pi/2) – Superposed fundamental
Sin(2t)+sin(t+pi/2) – superposed 2nd harmonic.
Etc.
Then all of the simple tones, superposed to give the resultant wave.
http://www.wolframalpha.com/input/?i=pl ... %2F2%29%29
Please note that is method of superposing the sum of the simple tones gives the exact same result as superposing the two complex tones.
It is therefore valid to analyse the dominant tones as simple sine waves to give an approximation of the sound.
Comparison of a Cosworth V8 (twin exhaust outlets) with the new V6 turbo (single exhaust outlet)
By taking a spectrograh of a recording of the two engines, we can see the frequency content. Please note this data is by no means good quality. It’s recorded from youtube, using a phone. It should be enough for us to determine the order content, and the dominant tones we hear.
Data was captured using SpectroLog app. Using 4410Hz sample FQ, for a range of 2200Hz.
Unfortunately, SpectroLog only outputs a dumb image of the spectrum, not the scales. The x scale is just a time (s). The Y scale is frequency in (Hz) (0 at the bottom and 2205 at the top). The Z scale is dB. I will highlight, the frequencies of interest.
Cosworth V8 - 20,000RPM dyno run.
http://www.youtube.com/watch?v=qLVp3SOKGJA
This run was used because it has a tacho on screen indication the rpm, there is also a nice couple of seconds of a steady 20k rpm. From 13 seconds. We will analyse this section.

The Area of Interest is highlighted in the block box, as this corresponds to 20,000rpm in the video.
1st Order @ 20krpm = 333Hz
2nd Order @ 20krpm = 666Hz (1/2 firing frequency)
3rd Order @ 20krpm = 999Hz
4th Order @ 20krpm = 1332Hz (firing frequency)
As we can see from the colourmap, there are many orders. The most dominant on the run-up, seems to correspond do 2nd, 4th, and 6th orders. 1.5order appears to be also present (500Hz).
So now we can compare the sine tones for half the firing frequency, and the firing frequency.
At 20,000rpm – 2nd Order (1/2 firing frequency) tone
http://www.wolframalpha.com/input/?i=pl ... 33*2pit%29
At 20,000rpm – 4th Order (firing frequency) tone
http://www.wolframalpha.com/input/?i=pl ... 2pit%29%29
Note that the format for creating a sine tone of a specific frequency and phase http://en.wikipedia.org/wiki/Sine_wave
It’s fairly clear that the pitch of the engine sounds much closer to the 666Hz sine tone. Indicating that it’s the half firing frequency you hear as the fundamental note.
Obviously this doesn’t show the full tone. So we can create a tone containing the three dominant engine orders. Plus the 1.5 order.
http://www.wolframalpha.com/input/?i=pl ... 33*2pit%29
The coefficients are affecting the amplitude of the wave to give approximately equal spectral power. This sound gives a fairly representative tone when compared to the video 13-14 seconds, even considering the orders present on the colourmap but omitted from the analysis.
Wolfram Alpha has trouble with sampling non integer sine waves, so it's tricky to get half orders to work. This does have implications in real life tones, such as http://en.wikipedia.org/wiki/Beat_(acoustics)
2014 Renault V6 Turbo
https://www.youtube.com/watch?v=g8jz_Dgb8D4
This run was used, because it’s the only sound we’ve got for the new engine! Unfortunately there is no tacho; so we must make an educated guess as to the orders.
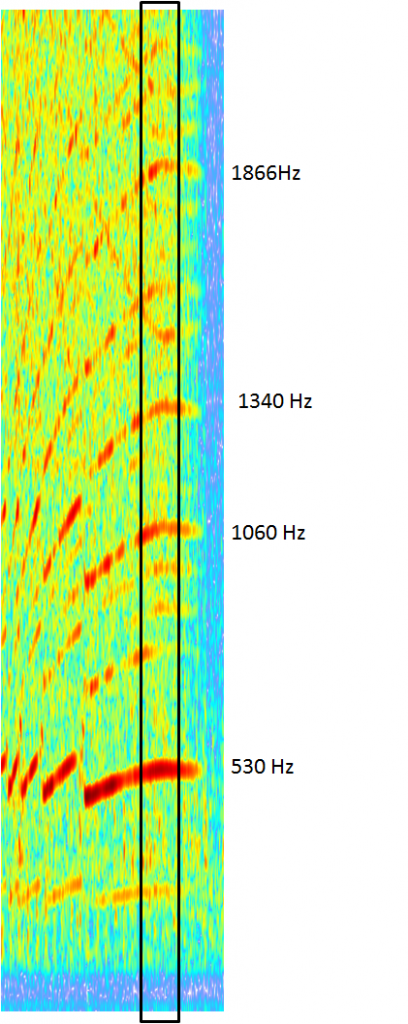
We will again choose the flat area for analysis. Dominant tones are indicated at 530Hz, 1060Hz, 1340Hz, 1866Hz. And various other minor orders. The fundamental dominant tone is 530Hz.
If we assume this is the full firing order for a V6 (3rd order). We get an rpm of 530/3*60 = 10,600rpm.
If we assume this is half firing order (1.5order). We get an rpm of 530/1.5*60 = 21,200rpm.
It seems clear that the full firing order is the more sensible, which is what we would expect with a single exhaust orifice.
This gives the orders:
1st order = 176.6Hz, 3rd order = 530Hz, 6th order = 1060Hz
The other two tones don't relate to engine firing, but are 7.6order and 10.5order.
The tone of the two engine orders:
http://www.wolframalpha.com/input/?i=pl ... 76*2pit%29
The tone of the engine orders + unknown contribution
http://www.wolframalpha.com/input/?i=pl ... 76*2pit%29
As you can see the introduction of the half order content gives a more 'correct' sound, as it creates auditory beats. (Again, Wolfram Alpha doesn't really like non-integer sine waves, so it's tricky to play with this just using this calculator)
Summary
We can build rudimentary models using a summation of sine tones to estimate the sound from an engine.
The V8 noise, with it's two separate exhausts has a fundamental note based on 2nd order (half firing frequency).
The V6 with it's single exhaust orifice has a fundamental note based on 3rd order (full firing frequency).
A post of Ciro proportions.
Comments and questions welcome.




