Hello Brian Coat.
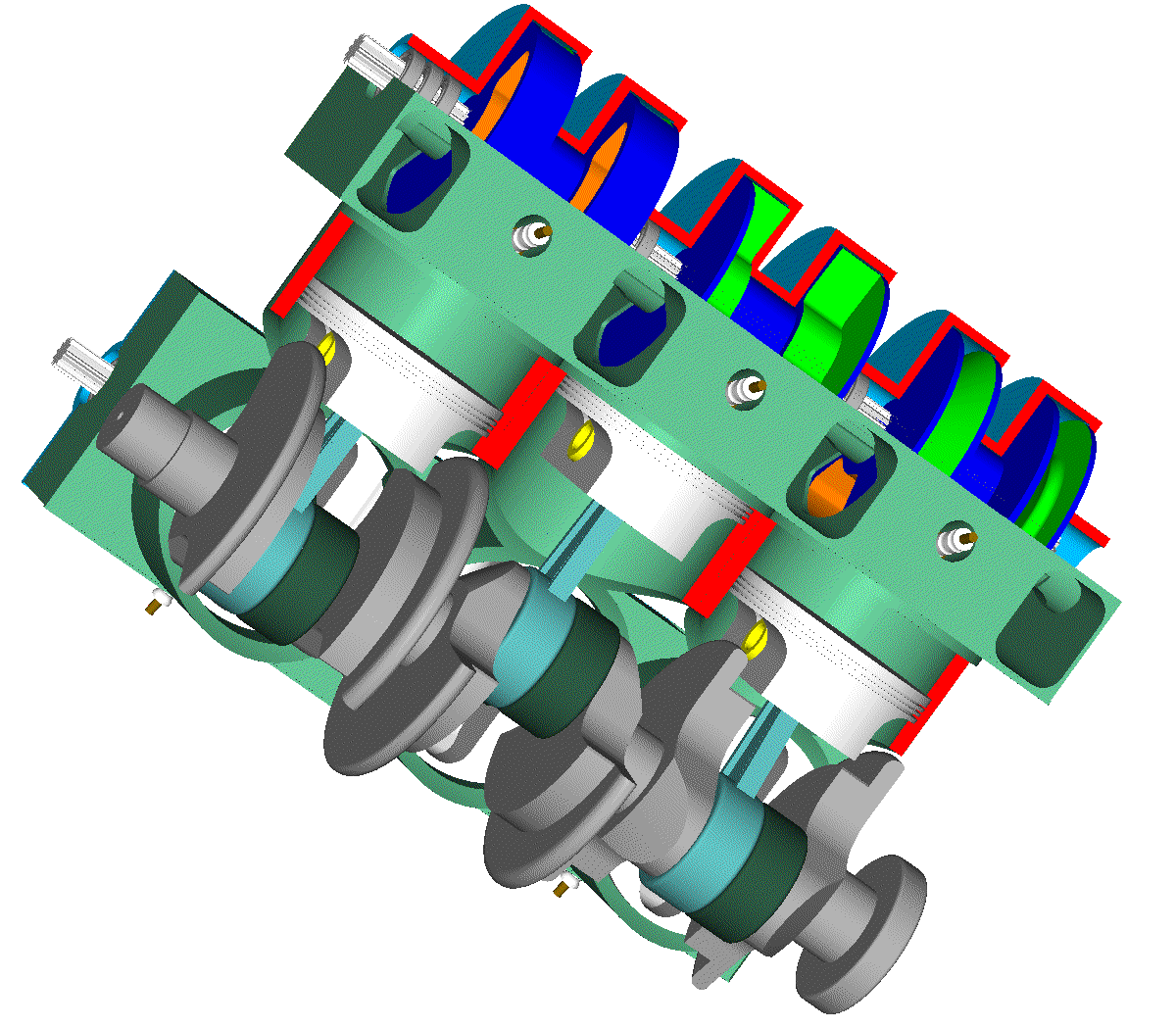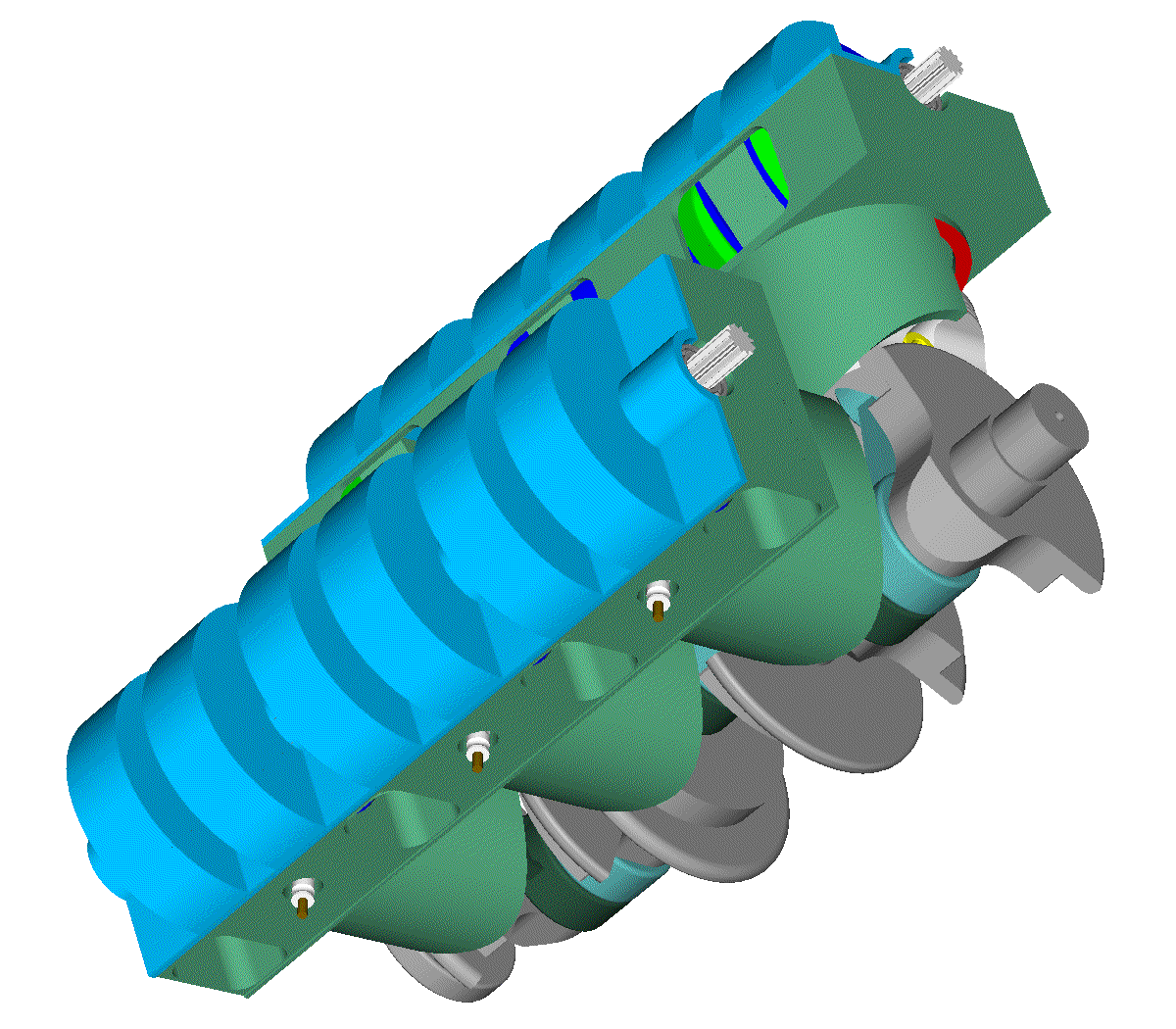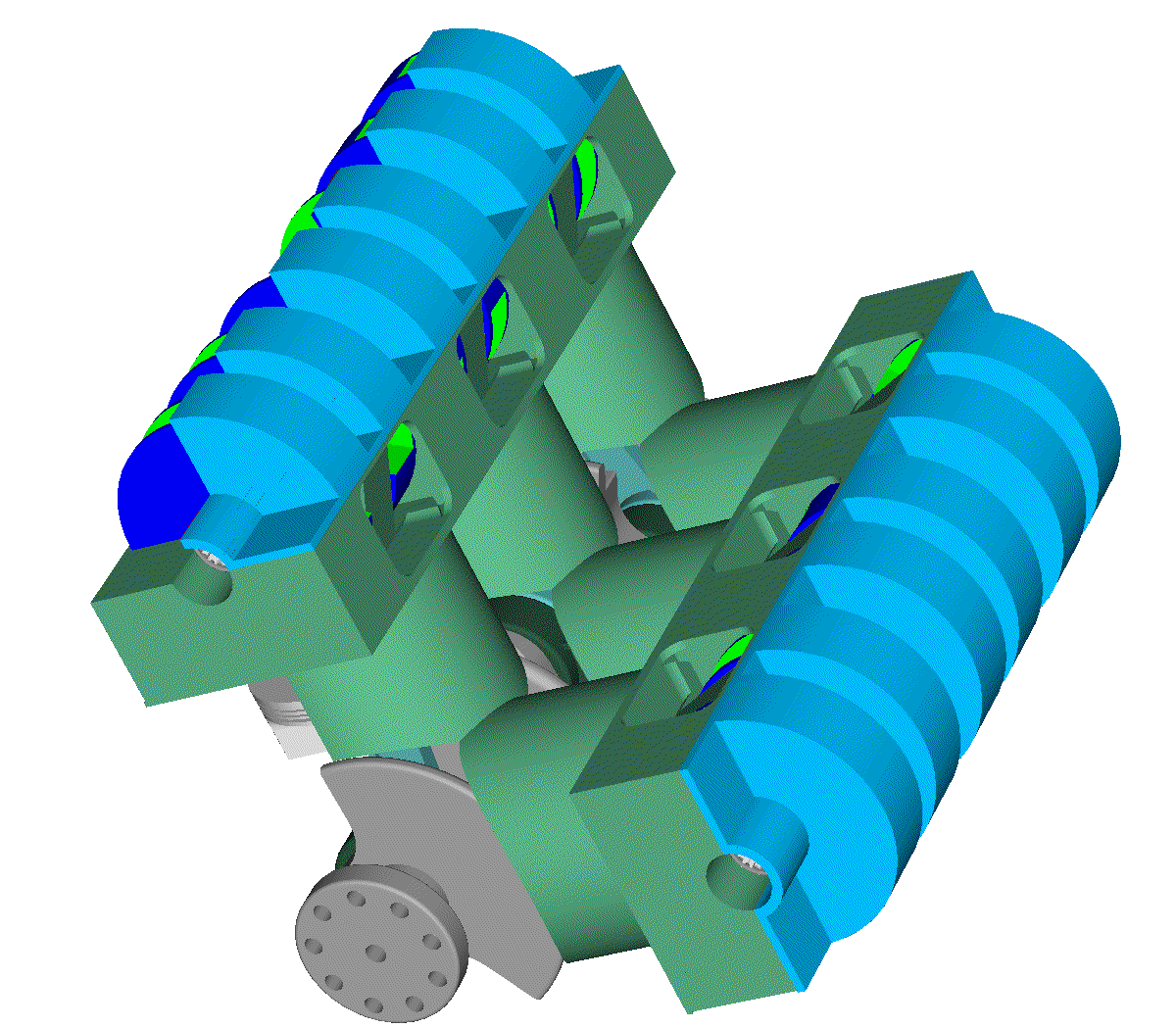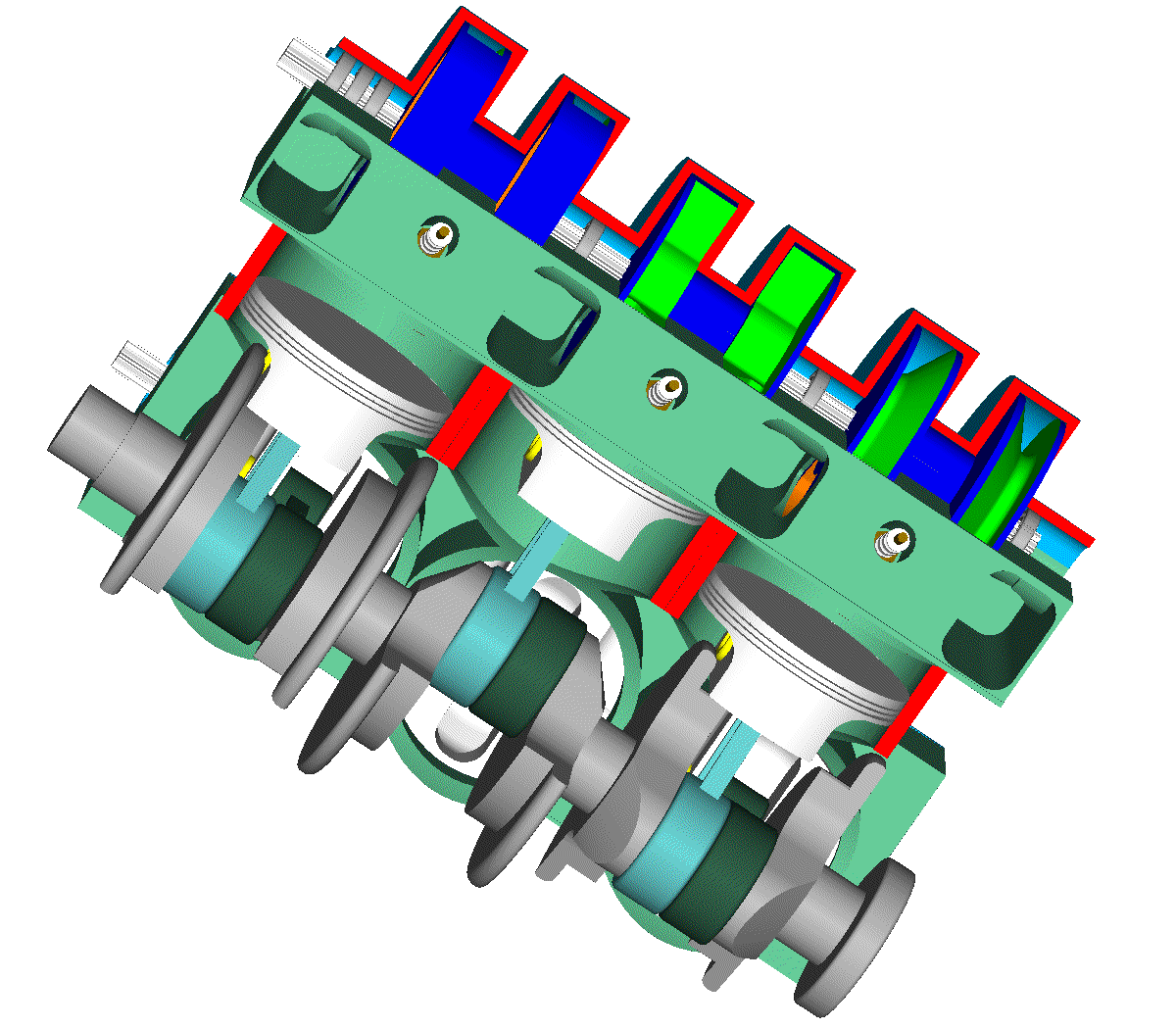
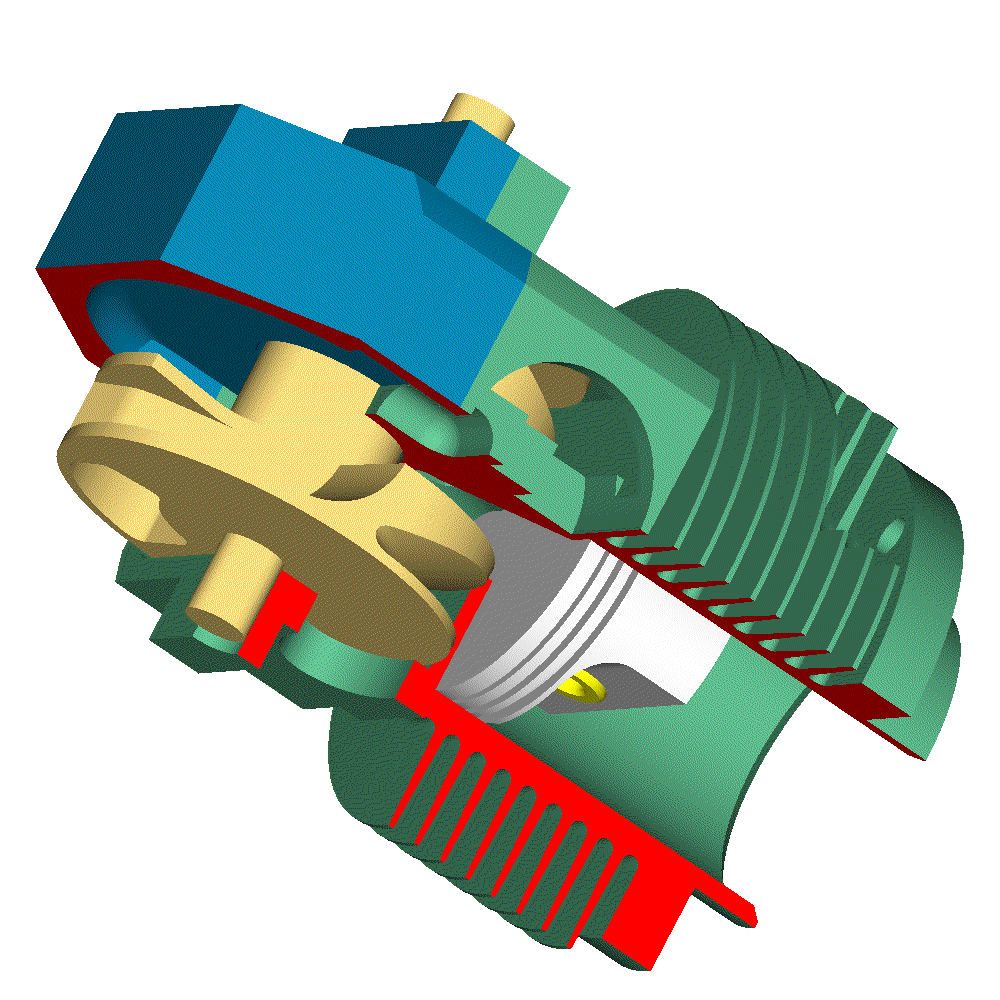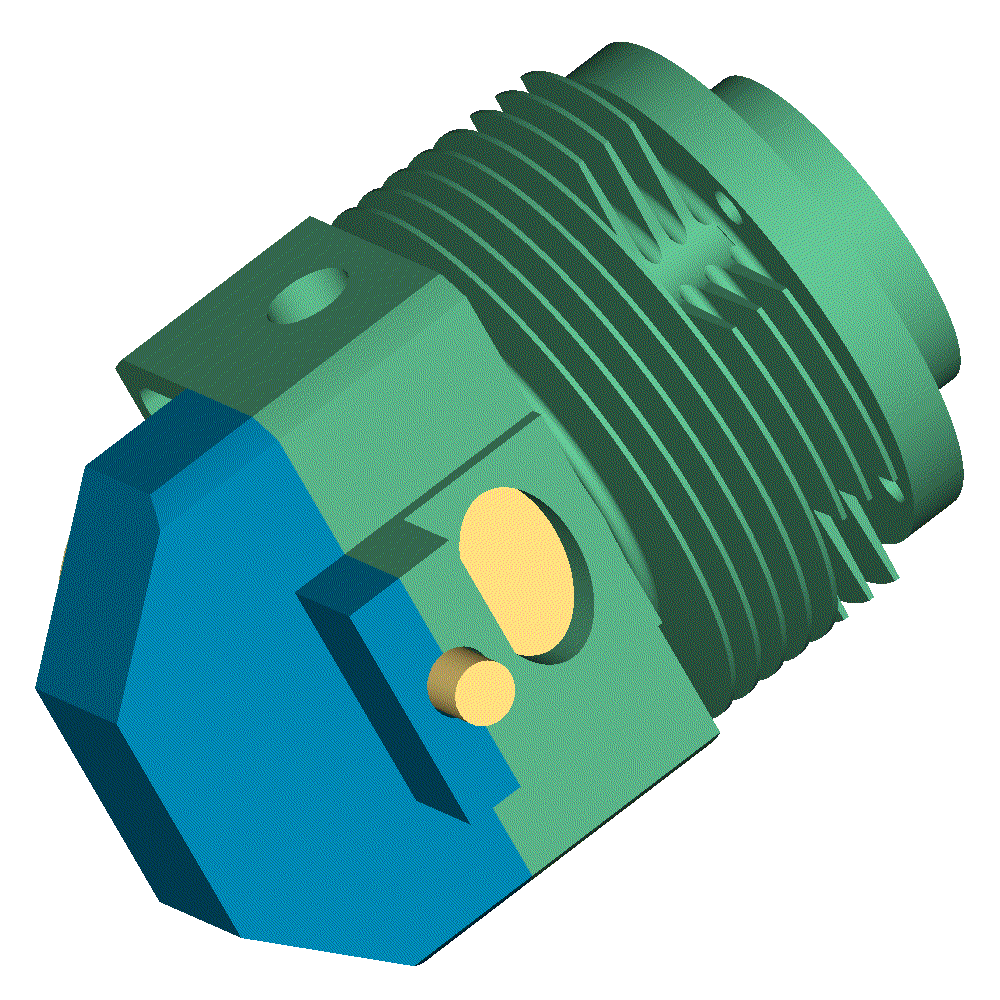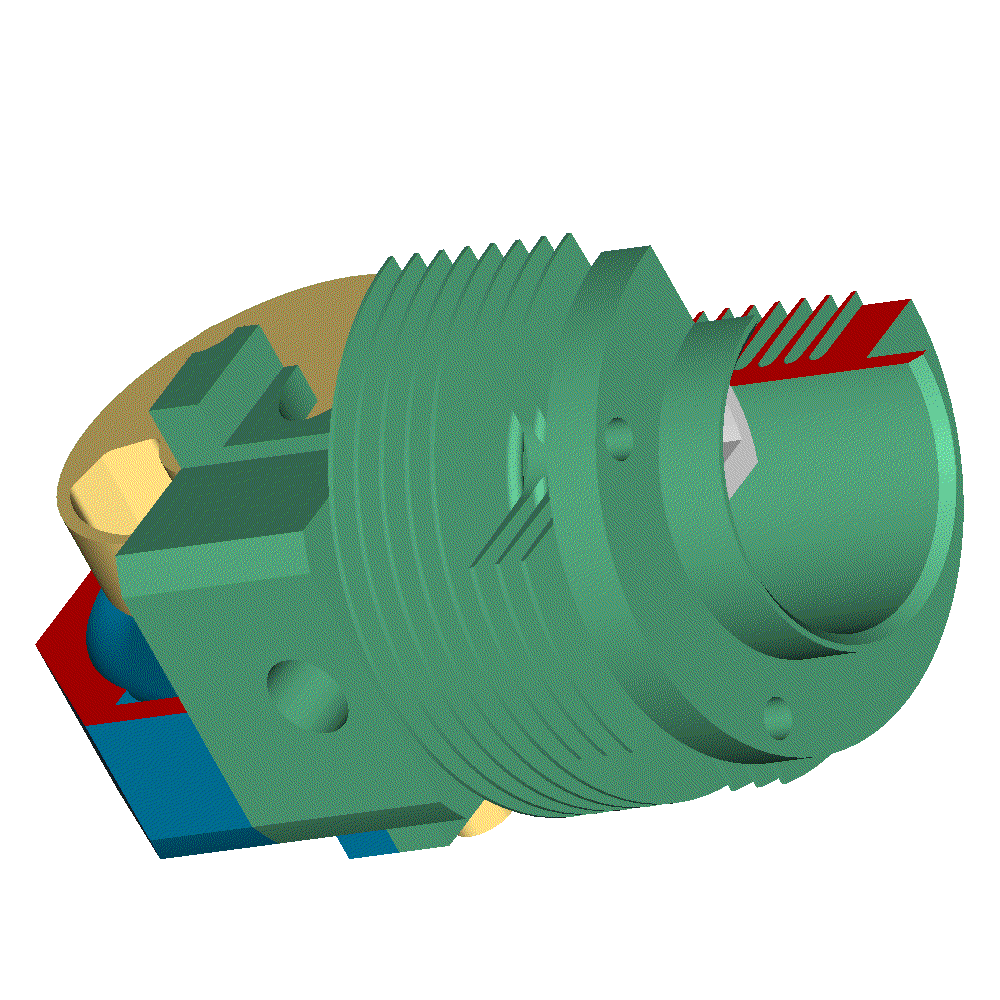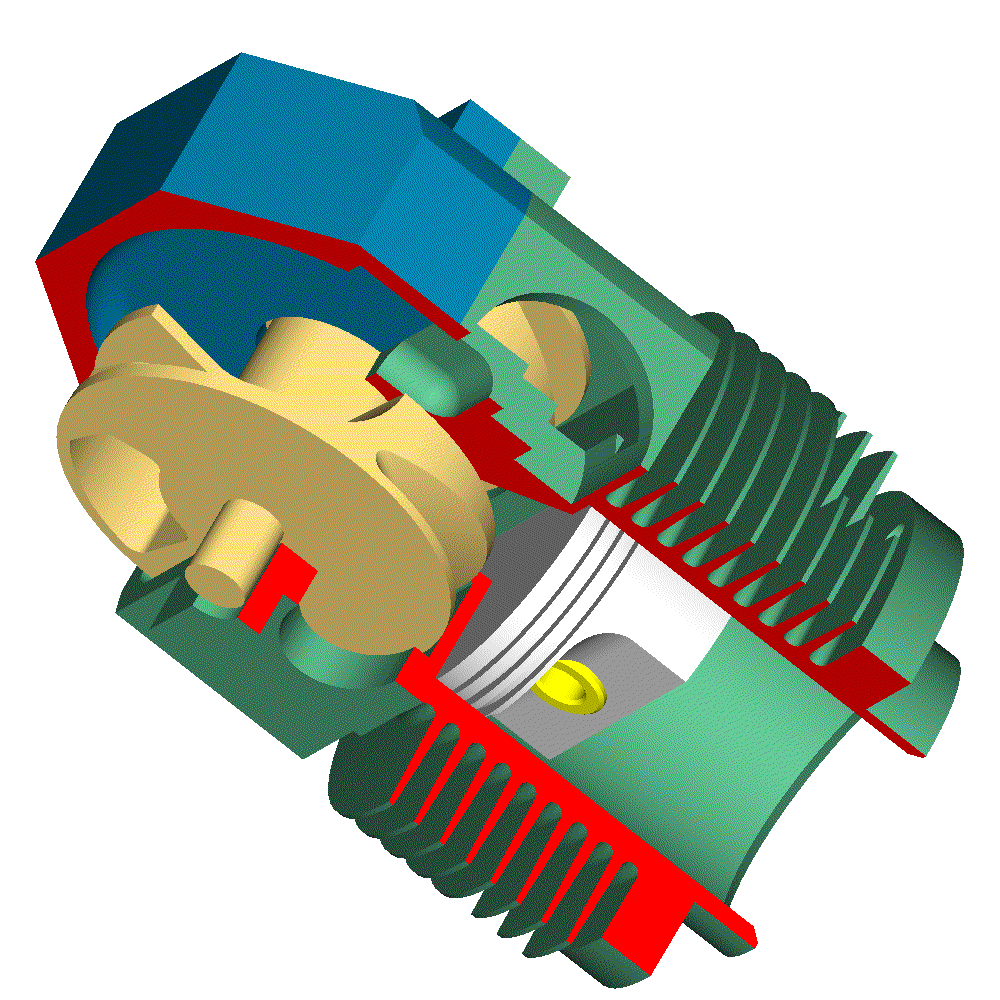
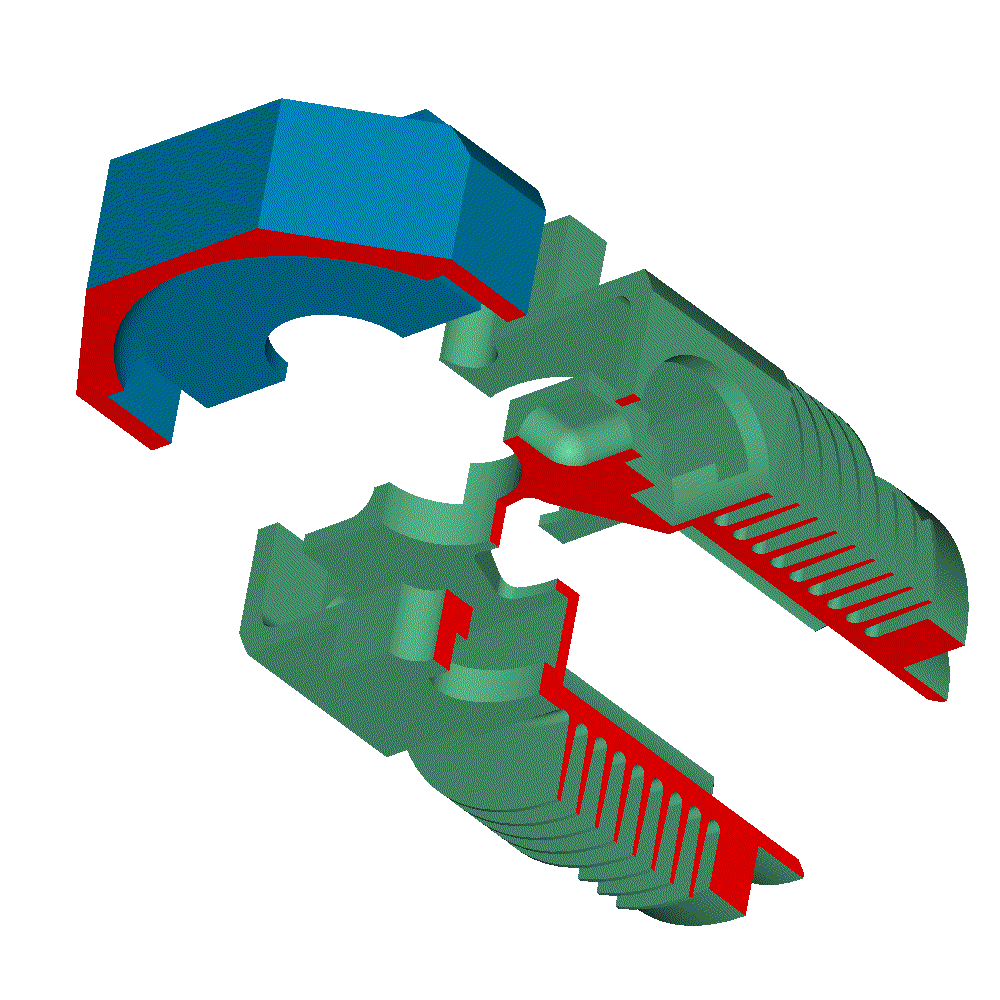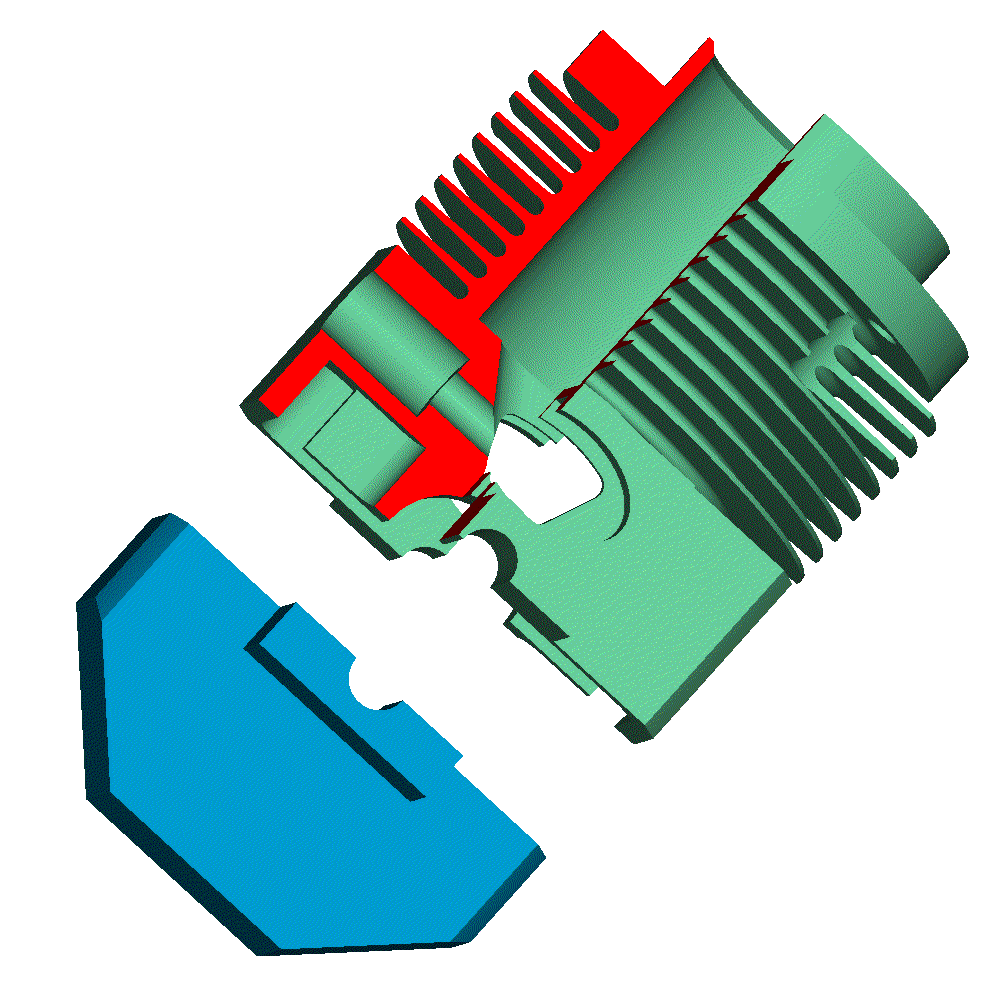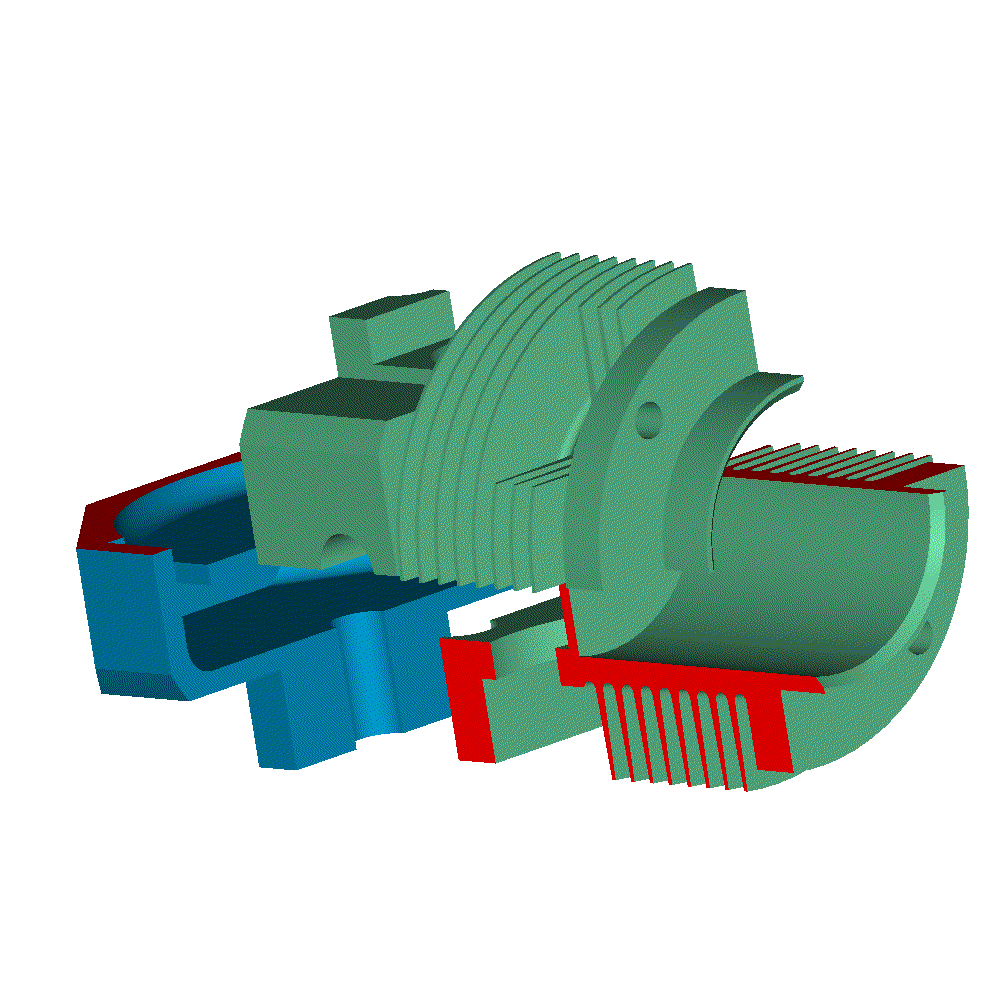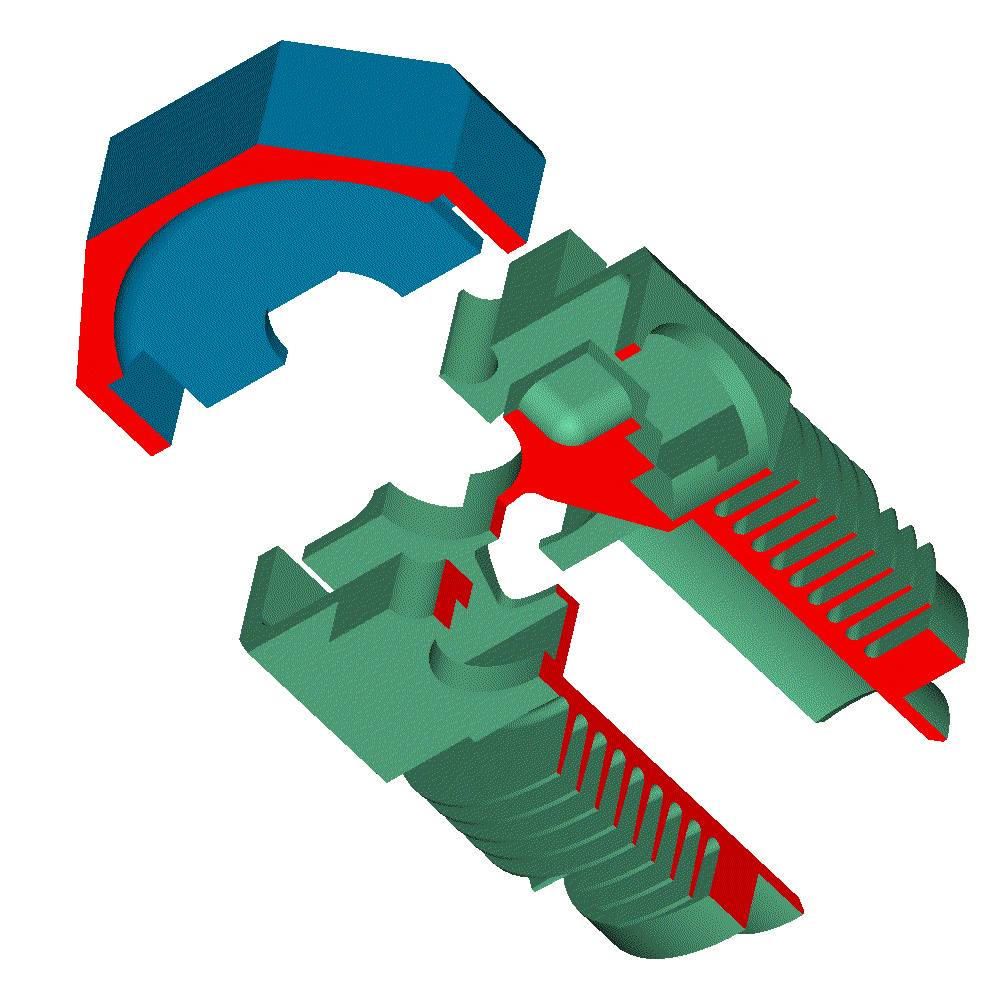
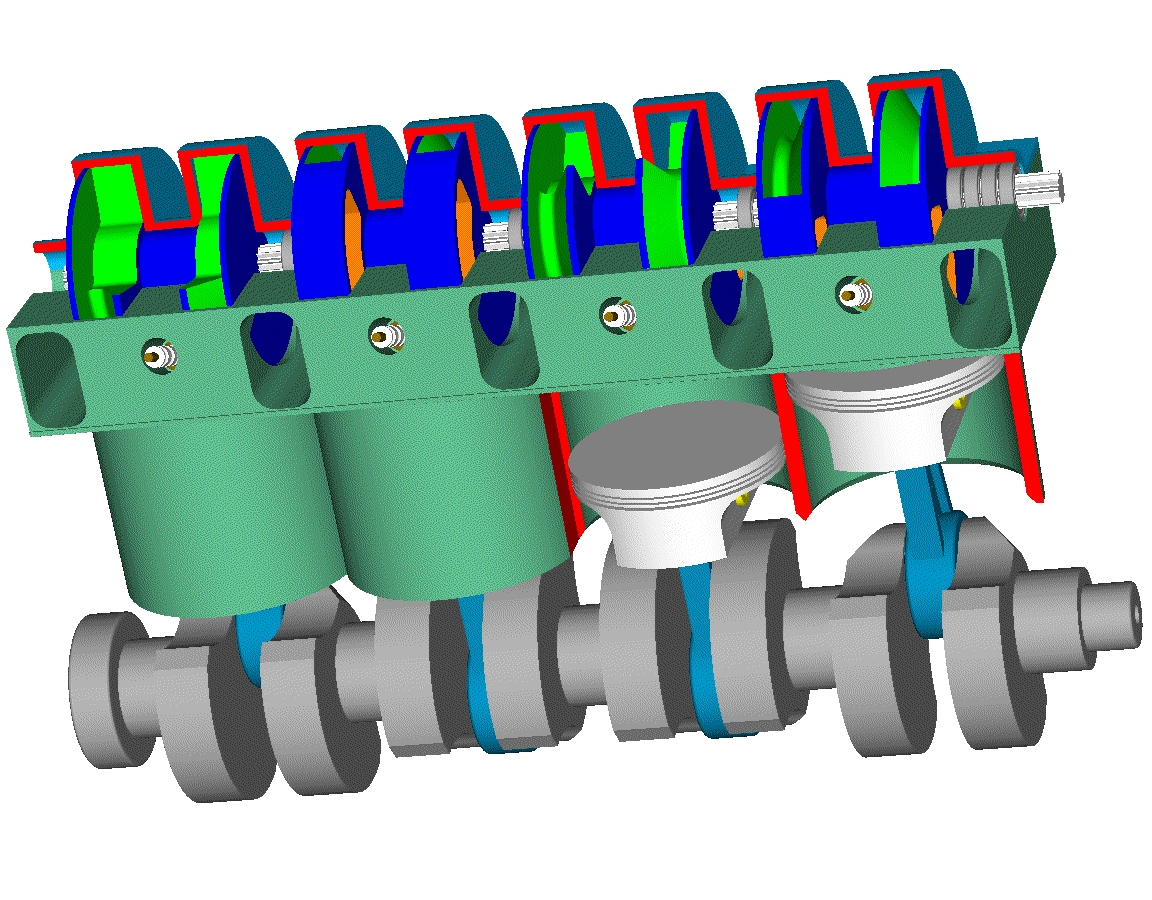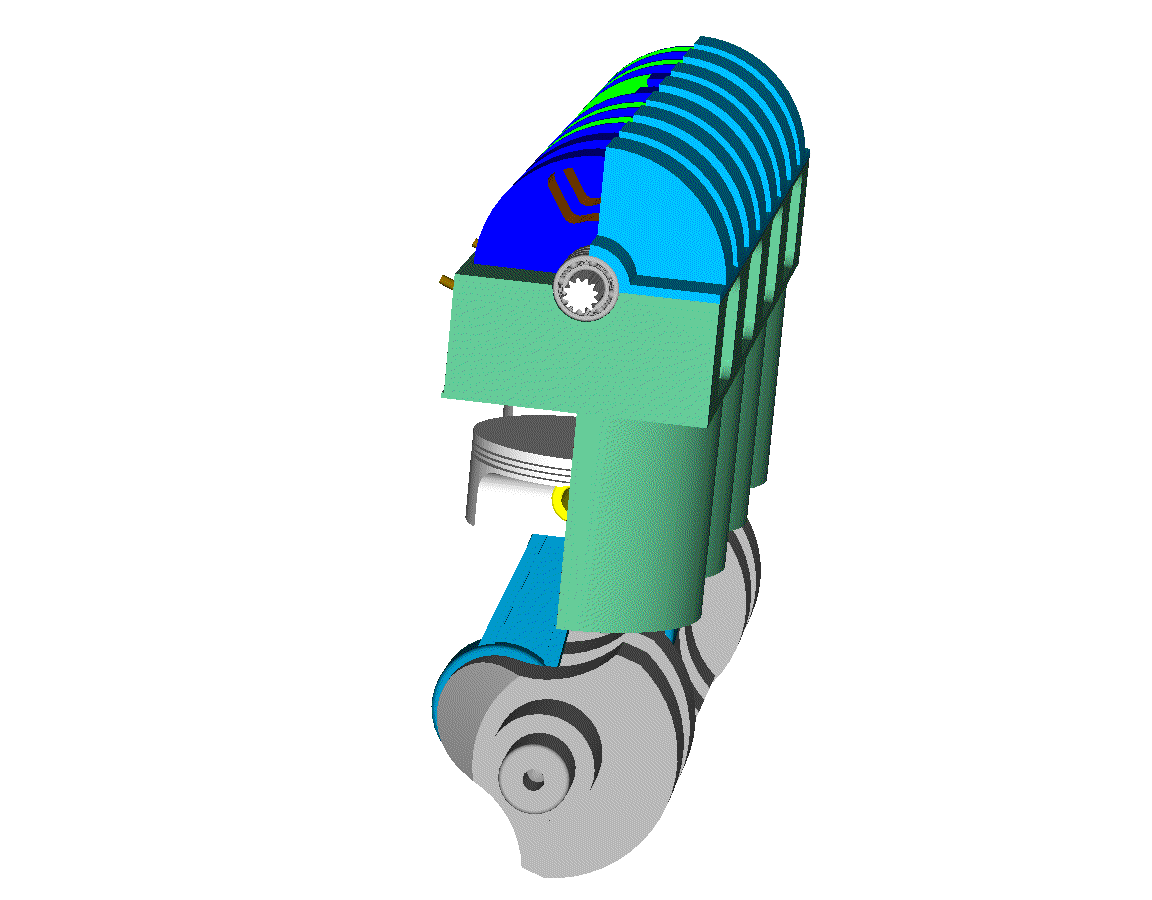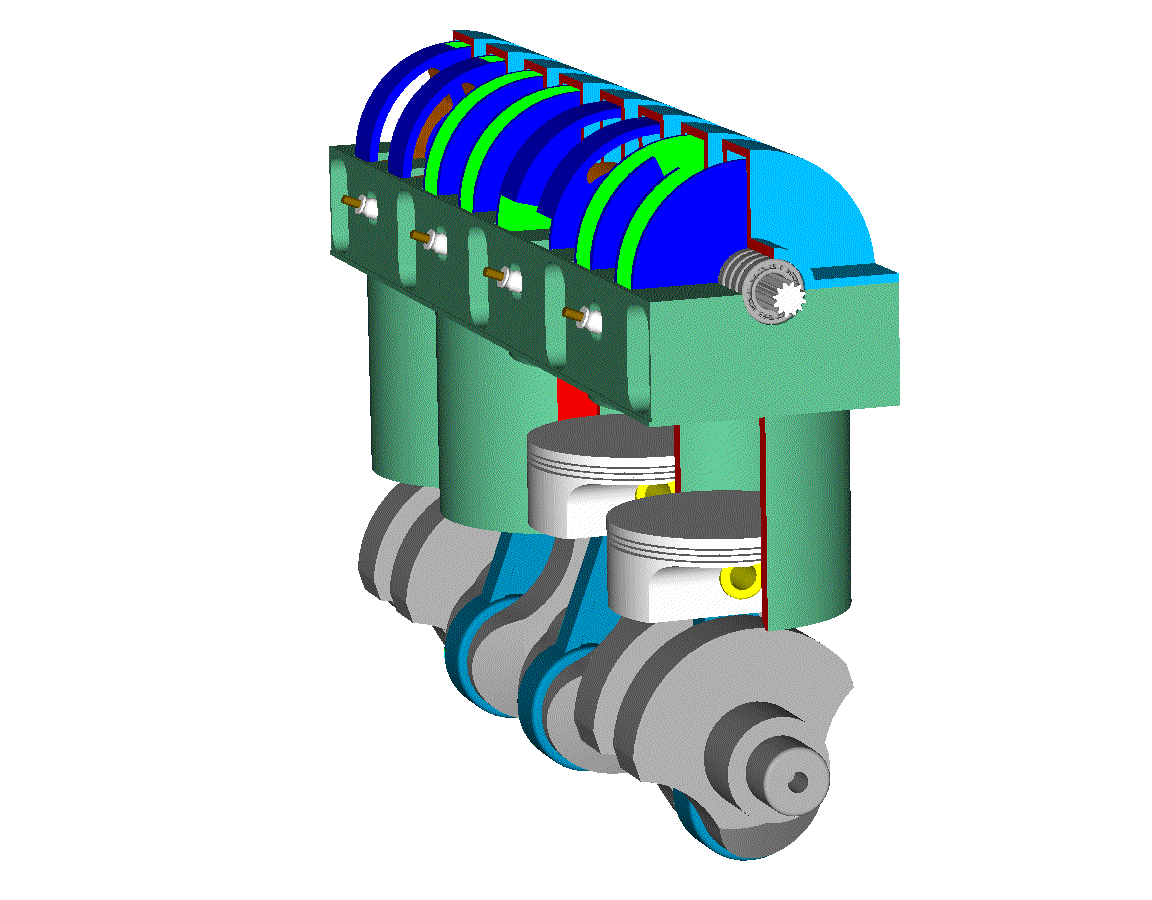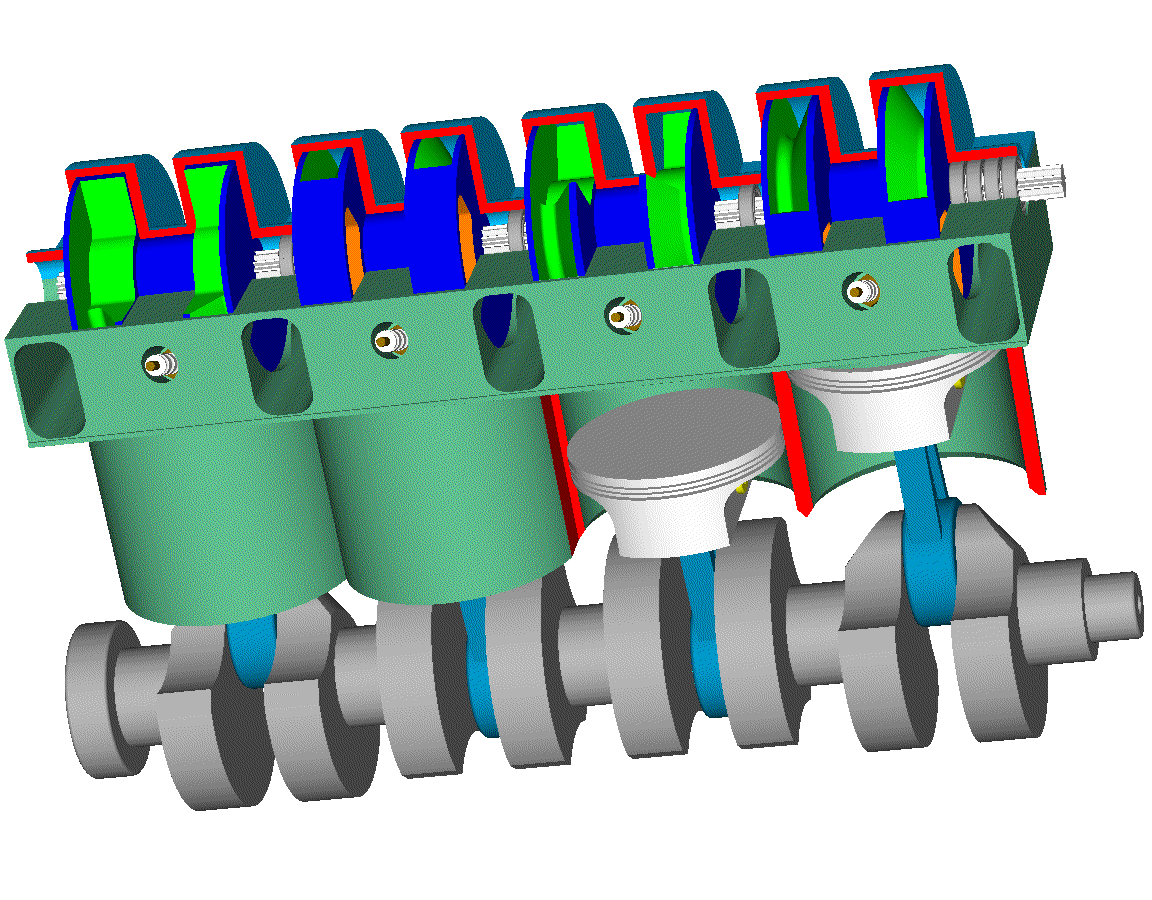
Let’s see the opening and closing of the valves of the Desmodromic cylinder head of the Ducati Panigale 1299 from the energy viewpoint (the previous analysis was based on a rough approximation of the force necessary for the motion) .
The valve lift is 16mm, the total “reciprocating” mass is taken 100gr.
The engine makes its peak power at 10,500rpm.
10,500rpm of the crankshaft means 1.5*10,500=15,750rpm for the valve reciprocation (in 240 crankshaft degrees the valve makes a full reciprocation) .
For simplicity the valve lift profile is taken as pure sinusoidal (any difference from the pure sinusoidal increases the required forces and the friction).
Initially the opening cam lobe has the control over the intake valve.
During opening, at the middle of its stroke the valve has a linear speed of 13m/sec (pi*0.016m*15,750/60). Its kinetic energy is 1/2 * 0.1Kg * (13 m/sec)^2 = 8.5J
This energy is provided to the valve by the opening camlobe through the opening rocker arm.
After the middle stroke the control of the valve passes to the closing camlobe.
When fully opened, the valve has zero kinetic energy. From the middle stroke to the full open position, the closing camlobe, through the closing rocker arm, absorbs the 8.5J of the valve (the valve has zero speed and so zero kinetic energy).
During closing, at the middle of its stroke the valve has again 8.5J kinetic energy; this energy came from the closing camlobe by means of the closing rocker arm.
After the middle of its stroke the control of the valve passes to the opening cam lobe, again. The opening camlobe decelerates the valve and absorbs the 8.5J of its kinetic energy.
In a second the valve opens and closes 0.5*(10,500/60)=87.5 times (the camshaft rotates with half crankshaft speed).
According the previous, during a second, 8.5+8.5=17J have passed between the valve and the camshaft 87.5 times. This is 1,5kW (2PS) for one valve.
There are 8 valves in total (the heavier exhaust valves have shorter stroke, so the kinetic energy is more or less the same with the kinetic energy calculated for the intake valves), which means 12kW (16PS).
The previous were calculated with 100% efficiency of the kinematic mechanism (in the meaning that in order the valve to absorb 8.5J kinetic energy, the camshaft provides only 8.5J energy).
If the Desmodromic valve train of the Panigalle 1299 operates with 50% energy recovery (quite doubtful) the power required for the valve train at 10,500rpm is 6kW (8PS).
If the Desmodromic valve train of the Panigale 1299 runs with 25% energy recovery, it requires 9kW (12PS) at 10,500rpm
Most of the friction is at the contact point between the rocker arms and the camlobes, and there is no way to have hydrodynamic lubrication there:

Spot on the big diameter "closing" camlobe and its rocker arm. Looking at it, I seriously doubt about its capacity to recover more than, say, 25% of the energy.
Now see the previous post with the extreme-over-square Ducati Panigalle with the 128mm bore, the 50mm stroke, the 10% bigger valves (17.7mm valve lift) and the 14,000rpm rev limit.
At 14,000rpm, 17.7mm valve lift and 20% heavier valves (0.12Kg instead of 0.1Kg, which is a small increase considering the 10% increase of the valve diameter), the maximum speed of the valve becomes 20m/sec,
which means a kinetic energy equal to 0.5*0.12Kg*(20m/sec)^2=24J.
24J+24J=48J and 0.5*(14,000/60)=116.7,
so the power required is: 48J * 116.7/sec = 5.6kW per valve,
which makes 45kW (60PS) for the eight valves of the two cylinder heads of the modified Panigale 1299.
This power has to reciprocate between the camshafts and the valves.
Depending on the energy recovery, the net power necessary for the valve train is calculated.
For instance, with 25% energy recovery, the valve train consumes 33kW (45PS), with 50% energy recovery the valve train consumes 22kW (30PS).
Even with 75% energy recovery the energy consumed by the valve train of the modified Panigale at 14,000rpm is 11kW (15PS).
Worth to mention: the timing chain has to be capable to pass the complete 60PS of power, no matter how much is recovered.
Do I miss something?
Is it out by one order of magnitude?
Thanks
Manolis Pattakos